
In order to reduce the measurement errors caused by the displacement adjustment of the PIV high-speed camera, the calibration plate process, and the experimental placement, the PIV flow field measurement needs to apply the surface self-calibration and volume self-calibration techniques to improve the measurement accuracy.
1. Self-calibration technology
1.1 Applicable Scenarios
PIV-2D3C Measurement
1.2 Causes of Error
When establishing the measurement space coordinate system, defining the coordinate origin O, and specifying the x and y axis directions in the plane, the calibration plane where the calibration plate is located does not coincide with the measurement plane where the laser sheet light is located , resulting in translation or rotation, which leads to reconstruction errors.
1.3 Technical Principle
Principle of correcting mapping function based on disparity vector field
1.4 Calibration process
The first step is to map the particle image to the calibration plane and calculate the disparity vector field.
In the second step, the triangulation method is used to determine the intersection of the light rays passing through both ends of the vector in the measurement space, and the least squares method is used to fit the intersection to obtain the expression of the measurement plane in the original calibration coordinate system.
The third step is to transform the original coordinate system so that the measurement plane becomes the plane of z=0, and calculate the translation and rotation of the calibration plane and the measurement plane.
The fourth step is to determine the physical coordinates of the intersection in the new coordinate system and fit the mapping function.
The fifth step is to iterate until the disparity vector field converges to a small enough size and obtain an accurate mapping function.
1.5 Calibration results
Before and after surface self-calibration, the particle distance deviation is reduced from 4.2159 pixels to 1.1903 pixels.
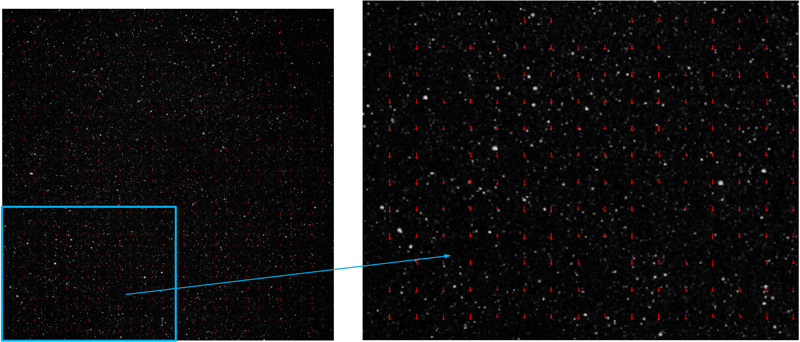
Figure 1 Before surface self-calibration (window size 64×64×64)
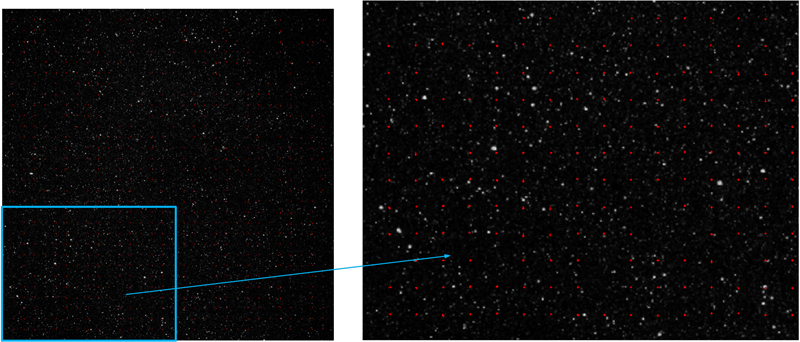
Figure 2 After self-calibration (window size 64×64×64)
2. body self-calibration technology
2.1 Applicable Scenarios
PIV-3D3C Measurement
2.2 Causes of Error
The calibration plate processing technology or the PIV camera displacement cannot be accurately positioned, resulting in the non-overlapping sight lines of particles under multiple views.
2.3 Technical Principle
Based on the principle of the small hole model reconstruction algorithm using third-order polynomials.
2.4 Calibration Process
The first step is to measure the pixel coordinate sets S1, S2, S3, and S4 of all the white patches of particles in the particle images under the four cameras.
The second step is to traverse the pixel coordinates of each particle in S1, map them into the volume space, and obtain a string of potential spatial coordinates.
In the third step, the latent space coordinates obtained are projected onto camera 2 to obtain a string of pixel coordinates. It is determined whether the pixel coordinates meet the matching conditions (within the line of sight, the distance line is less than a certain threshold, and the projection point falls within the line segment). If they meet the conditions, the particle space coordinates can be determined. If not, return to the second step to analyze the next particle. The space coordinates of the successfully matched particles are projected onto camera 3 and camera 4 for further verification. If the projection points are located at the corresponding particle pixel coordinates in S3 and S4, the match is successful. Otherwise, return to the second step. Repeat the above process until all successfully matched particles are located.
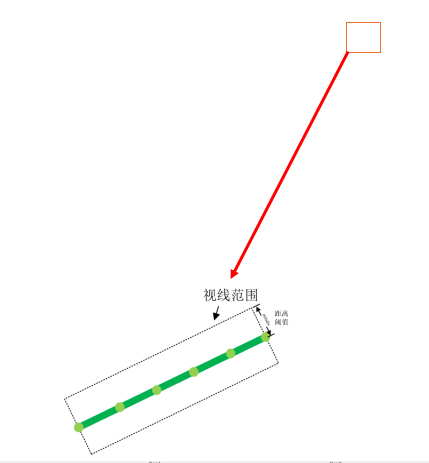
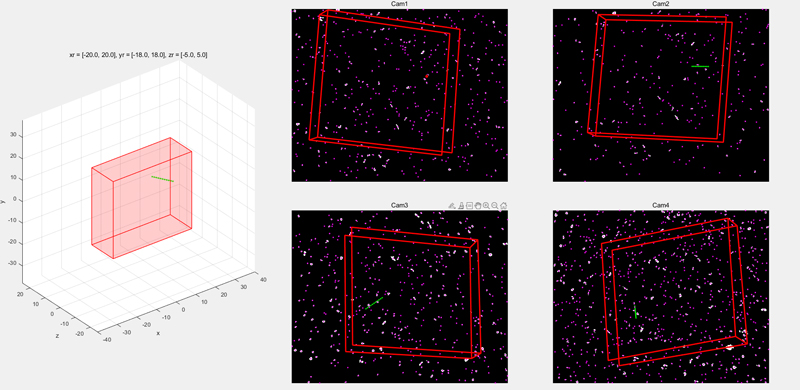
Figure 3 Schematic diagram of pixel coordinate matching
The fourth step is to establish a third-order polynomial algorithm optimization model to solve the optimal particle spatial coordinates (X, Y, Z) with the minimum average reprojection error.
The fifth step is to inversely solve and update the calibration model parameters according to the new spatial position.
The sixth step iterates until the reprojection error reaches a stable convergence state.
2.5 Calibration results
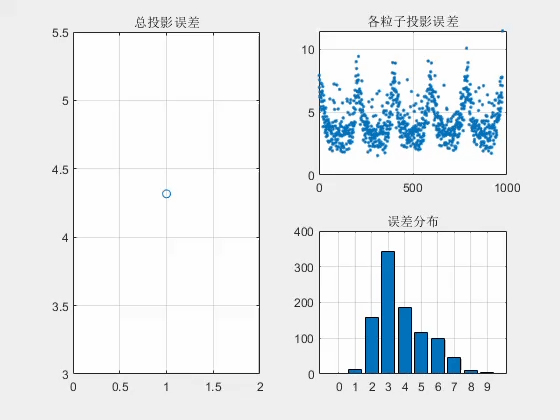
Before volume self-calibration, the total projection error is distributed around 3 to 4 pixels. After three rounds of iterative convergence, the error is stabilized at around 1 pixel, of which the error < 1 pixel accounts for 65%.
3. Conclusion
The RFlow 2D3C and 3D3C particle image velocimetry software integrates the above self-calibration technology to help fluid mechanics researchers obtain accurate representation of the three-dimensional velocity vector field of tracer particles in planar three-dimensional space and volume space.